Optical Constants
Thickness measurements are not independent of the optical constants. The film thickness affects the path length of light traveling through the film, but the index determines the light waves’ velocity and refracted angle. Thus, both contribute to the delay between surface reflection and light traveling through the film. Both n and k must be known or determined along with the thickness to get the correct results from an optical measurement.
The optical constants for a material will vary for different wavelengths and must be described at all wavelengths probed with the ellipsometer. A table of optical constants can be used to predict the material’s response at each wavelength. However, it is not very convenient to adjust unknown optical constants on a wavelength-by-wavelength basis. It is more advantageous to use all wavelengths simultaneously. A dispersion relationship often solves this problem, by describing the optical constant shape versus wavelength. The adjustable parameters of the dispersion relationship allow the overall optical constant shape to match the experimental results. Compared to fitting individual n, k values at every wavelength, this greatly reduces the number of unknown “free” parameters.
For transparent materials, the index is often described using the Cauchy or Sellmeier relationship. The Cauchy relationship is typically given as:
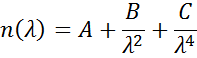
where the three terms are adjusted to match the refractive index for the material. The Cauchy is not constrained by KK consistency and can produce unphysical dispersion. The Sellmeier relationship enforces Kramers-Kronig (KK) consistency, which ensures that the optical dispersion retains a realistic shape. The Sellmeier relationship can be written as:
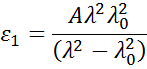
Absorbing materials will often have a transparent wavelength region that can be modeled with the Cauchy or Sellmeier. However, the absorbing region must account for both real and imaginary optical constants. Many dispersion relationships use oscillator theory to describe absorption for various materials. These include the Lorentz, Harmonic, and Gaussian oscillators. They all share similar attributes, where the absorption features are described with an Amplitude, Broadening, and Center Energy (related to frequency of light). Kramers-Kronig consistency is used to calculate the shape of the real component after the imaginary behavior is described by the oscillator. An offset to the real component is added to account for extra absorption outside the measured spectral region. The Lorentz oscillator can be written as:
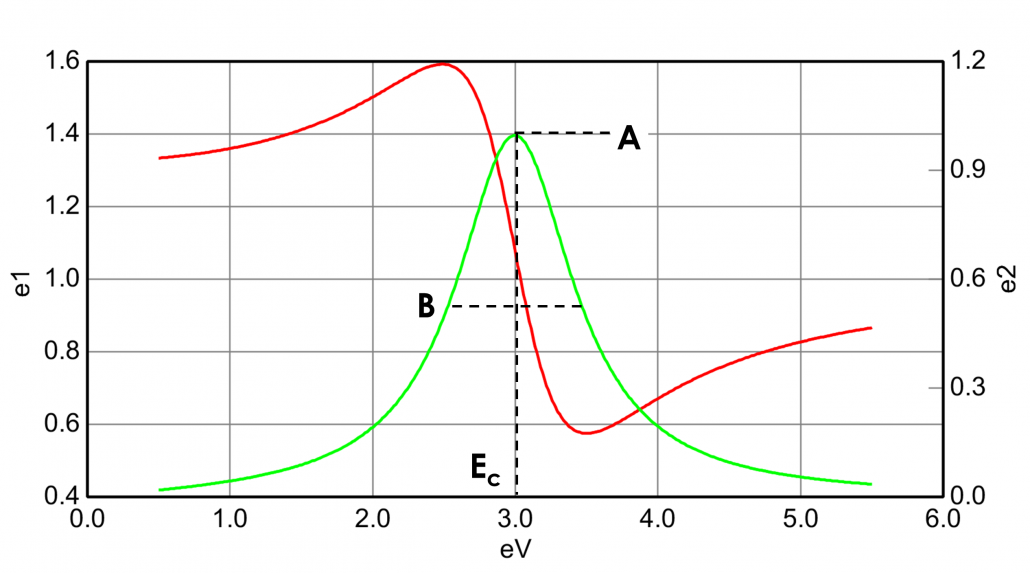
![]()
where the parameters for Amplitude (A), Broadening (B), Center Energy (Ec), and offset (e1, offset) are also shown in Figure 13 for a typical Lorentz oscillator. The energy, E, is related to the frequency of a wave, n:
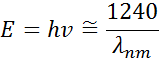
where h is Planck’s constant and the wavelength, l, is given in nanometers. More advanced dispersion models, like the Tauc-Lorentz and Cody-Lorentz, will include terms to describe the bandgap energy.